Invasion Zombie
Hola!, este es mi primer post en Omegaup y voy a describir mi solución para el problema Invasion zombie. Hace un año encontré este problema, me pareció interesante y logre resolverlo, aunque algo tricky. Hace unos días me tope con este problema nuevamente y lo resolví por segunda ocasión, pero con una solución más simple, al menos eso creo.
Primer solución aliases: [’/invasion-zombie']
La idea principal tanto en la primera como en la segunda solución es diseñar una función $latex f(d)$ que nos retorne el número de colonias infectadas después de $latex d$ días, nos interesa el mínimo valor de $latex d$ tal que el número de colonias infectadas sea mayor o igual a $latex C$. Una propiedad importante es la siguiente, $latex f(d)$ nunca decrece, es decir $latex f(d) <= f(d+1)$. Esta propiedad nos permite utilizar búsqueda binaria para encontrar las respuesta en $latex O(\lg_{2}(n))$. Diseñar una función que determine el número de colonias infectadas, dependiendo del background de cada uno, es la parte interesante, y es donde difieren las dos versiones, bueno, un poco. Este es el código de la primer versión, no voy a entrar en detalles porque ni yo me acuerdo bien que trucos aplique, pero la idea es parecida a la de la de la segunda versión, lo que cambia es la estrategia.
Segunda versión aliases: [’/invasion-zombie']
Bueno, empecemos, trascurridos $latex d$ días, ¿cuántas colonias han sido infectadas? Simulemos la invasión y veamos si podemos encontrar un patrón.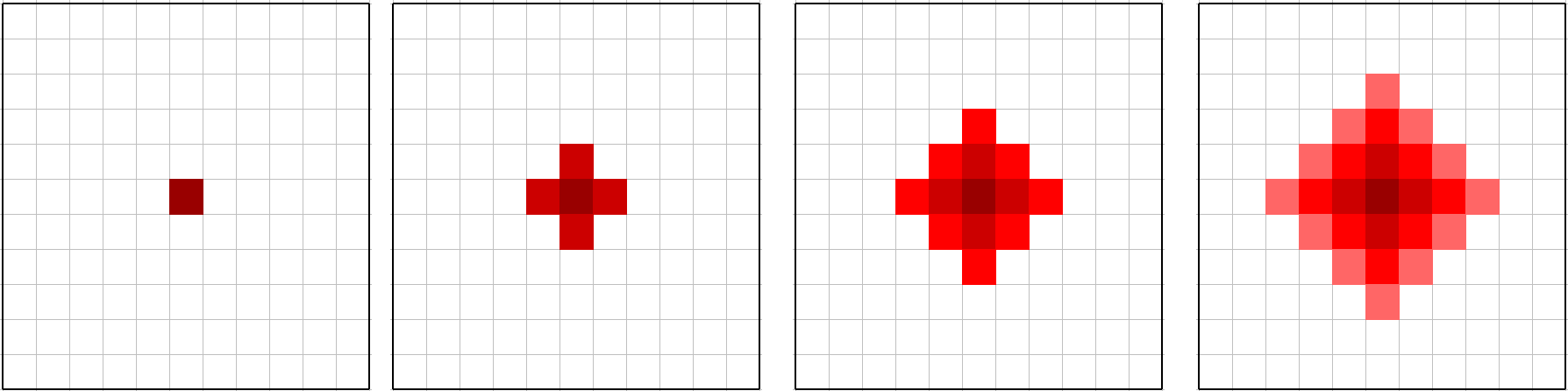 
No es complicado llegar a la siguiente fórmula: $latex f(d) = d^{2} + (d+1)^{2}$ Si el espacio de la ciudad fuese ilimitado nuestra función de verificación sería algo parecido a:
Sin embargo, el espacio de la ciudad es limitado y habrá casos como los siguient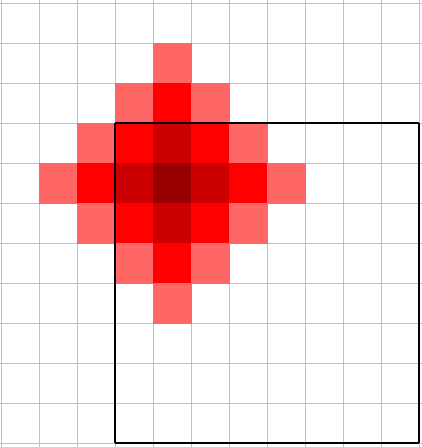es: 
Entonces nuestro objetivo es encontrar el área delimitada por la ciudad (un cuadrado de N * N unidades), lo cual se pone un poco tricky. La siguiente imagen nos ayudará a entender el código de la solución sin entrar en tantas explicaciones.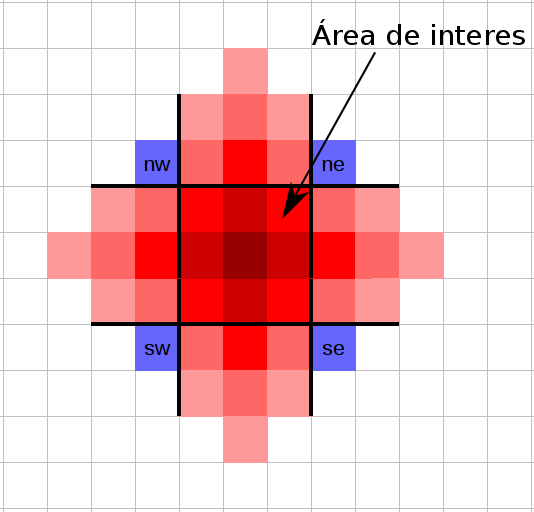 
Es decir, el área total menos el área de los triángulos superior, inferior, izquierdo y derecho. Obsérvese que los triángulos pueden traslaparse y por lo tango estaríamos restando esas áreas 2 veces, por ello tenemos que calcular las áreas de traslape (nw, ne, se y sw en la imagen) y regresar lo a la suma total. Lo que sigue es la implementación:
Espero que les sea útil, dudas, comentarios o correcciones son bienvenidas.