Soluciones de la Fase 1 de la Liga de Programación omegaUp

Problema A

Para este problema, consideramos un arreglo de ocurrencias $O$ sobre los elementos del arreglo. De modo que la respuesta está dada por

$\sum\limits_{i=A}^B O_{i}$

Problema B

Si consideramos el mismo arreglo de ocurrencias $O$ sobre los elementos del arreglo, la respuesta está dada por $O_k$.

Podemos generar todos los elementos de la secuencia de Fibonacci hasta $30000$, y guardarlos en un mapa $M$, de modo que $M_k = 1$ si $k$ es un elemento de Fibonnaci, y $M_k = 0$ en caso contrario. Generamos la respuesta simplemente iterando desde $i = 4$ hasta $i = N - 1$, e imprimimos $i$ si $M_i = 0$.

Problema D

La clave para este problema, es usar variables que no provoquen un desbordamiento, por ejemplo, unsigned long long. Luego, es conocido que la serie de Fibonacci crece rápidamente, lo suficiente, como para generar la secuencia con todos sus elementos menores o iguales a $N$, guardando por cada uno su respectiva posición en ella. Por lo tanto, basta con checar si $N$ es un elemento, e imprimir su posición. En caso de no serlo, imprimimos $-1$.

Problema E

Este tipo de problema es conocido como straight-forward. Podemos guardar las estaciones de radio, y checar cuál estación es la mas cercana a la frecuencia dada, con una simple resta. En caso de haber dos estaciones con la misma distancia, la respuesta es la mayor. Solo debemos cuidar que la frecuencia esté dentro del rango permitido.

Problema F

En este problema lo que tenemos es un grafo dirigido acíclico con aristas pesadas (intuitivamente, es un árbol, sin la propiedad de que cualquier par de nodos estan conectados por un único camino). Los vértices son los eventos temporales, las aristas son dirigidas de $p_i$ a $i$, y su peso es $d_i$. Además, cada vértice contiene un valor extra $r_i$. Un grafo que podemos asociar al primer caso de ejemplo es el siguiente.

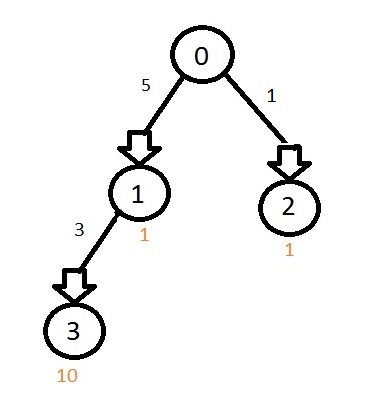
Sean $v_1$ y $v_k$ dos vértices distintos, tales que $v_1$ es ancestro de $v_k$. Es decir, existe un camino $v_1 \rightarrow v_2 \rightarrow \ldots \rightarrow v_k$ en el grafo. Definimos $S(v_1, v_k)$ como

$\sum\limits_{i=1}^{k - 1} d_{v_i}$

Es decir, la suma de los pesos en las aristas del camino. De modo que el problema se convierte en: Para cada vertice $v$, contar cuántos vértices $u$ en su “subárbol” $\;$ existen tales que

$r_u - S(v, u) \geq 0 $

Porque esto siginifica que tenemos suficientes segundos para viajar por el tiempo desde $u$ hasta $v$.

Consideremos un arreglo $E$, donde la entrada $E_v$ guarda cuántos descendientes $u$ de $v$ satisfacen

$r_u - S(v, u) \geq 0 $

Pero

$r_u - S(p_v, u) < 0 $

Donde $p_v$ es el padre de $v$. Si $v = 0$, entonces no hace falta considerar a su padre, puesto que no podemos viajar por el tiempo a algún ancestro de $0$ (ya que ni siquiera existe alguno).

En otras palabras, $E_v$ guarda cuántos descendientes de $v$ llegan a lo mas al vértice $v$.

También consideremos un arreglo $D$, donde la entrada $D_v$ guarda cuántos descendientes $u$ de $v$ satisfacen

$ r_u - S(v, u) < 0 $

Es decir, $D_v$ guarda cuántos descendientes de $v$ no pueden llegar al vertice $v$.

Y además mantengamos un arreglo $T$, donde la entrada $T_v$ guarda el tamaño del “subárbol” de $v$ (incluyendo a $v$). En otras palabras, cuántos descendientes tiene $v$ en total mas el mismo.

Por lo tanto, la respuesta final para el vértice $v$ está dada por

$(T_v - 1) - \sum\limits_{v \rightarrow u} (E_u + D_u)$

donde $u$ es un hijo directo de $v$. Ya que esto calcula cuántos descendientes de $v$ si pueden llegar a $v$.

Para el cálculo de nuestros arreglos, hacemos una dfs sobre el “árbol” (partiendo del vertice 0). Para cada vértice $u$, hacemos una búsqueda binaria sobre un arreglo que mantenga la suma acumulada de los costos sobre las aristas que forman parte del camino de $0$ a $u$, que nos devuelva el máximo ancestro $v$ al que podemos llegar desde $u$. Lo que nos dice que $E_v$ actualiza su valor a $E_v + 1$ (inicialmente, $E_1 = E_2 = \ldots = E_n = 0$). Esto se puede hacer usando un arreglo global. La idea es añadir la suma acumulada, luego explorar recursivamente el subárbol de $u$, y luego quitar la suma acumulada que añadimos. Esto es particularmente sencillo si usamos un vector de la STL para el arreglo global.

El arreglo $T$ se calcula facilmente en la misma dfs, ya que

$T_v = 1 + \sum\limits_{v \rightarrow u} (T_u)$

Ahora podemos generar $D$, al estilo de programacion dinámica usando $E$. Notemos que

$D_v = \sum\limits_{v \rightarrow u} (E_ u + D_u)$

Lo que se puede hacer en la misma DFS.

Por lo tanto, nuestro algoritmo tiene complejidad $O(Nlog(N))$.

Problema G

Primero reescribamos la expresión dada como

$k = \dfrac{xy}{x + y}$

De donde podemos despejar $y$ como

$y = \dfrac{xk}{x - k}$

Sin perdida de generalidad, supongamos $x \leq y$, entonces se tiene

$x \leq \dfrac{xk}{x - k}$

$x^2 \leq 2xk$

$x \leq 2k$

Por lo tanto, podemos iterar $x$ desde $1$ hasta $2k$, obtenemos $y$, y verificamos que $k = \dfrac{xy}{x + y}, y > 0$.

Guardamos las parejas que satisfazcan dichas condiciones y las imprimimos en el orden requerido, cuidando no repetir alguna respuesta.

Lo que nos deja con un algoritmo de complejidad $O(k)$.

Una solución alternativa es la siguiente:

Te puedes dar cuenta que $x, y > k$, entonces el problema se convierte a buscar $a$ y $b$ que cumplan

$\dfrac{1}{k} = \dfrac{1}{k + a} + \dfrac{1}{k + b}$

con $a,b > 0$. Si simplificas la igualdad llegas a que $k^2 = ab$, así que todo se reduce a encontrar las parejas de divisores $a, b$ de $k^2$. Lo que deja también un algoritmo de complejidad $O(k)$.

Nota: Agradezco a José Tapia y a Carlos Galeana por su colaboración en el problema $G$.