Solución a "K-Arbol"
Concurso: Preselectivo para la IOI 2013, Etapa 1, Examen 5 **Autor: **Saul de Nova Caballero
En pocas palabras el problema es, dado un árbol que se puede colorear, encuentra la menor solución satisfaciendo las restricciones dadas sobre los colores. Este problema es un caso particular de Graph Coloring(en español coloración de grafos), en donde el grafo es un árbol.
Subcaso 1(10 puntos)
Para el primer subcaso era posible hacer una búsqueda en profunidad sobre todos los nodos, encontrando la menor solución. Para guardar el árbol, era posible utilizar una matriz que guardara todos los colores posibles y entonces ver si era posible una solución con el menor color posible. La solución de este caso era trivial si se usaba una búsqueda exhaustiva.
Subcaso 2(20 puntos)
Para el segundo subcaso era necesario una mejor estrategia. Para este caso, era necesaria la observación de que todos los colores de los nodos solo dependen de su padre y de sus hijos. Otra observación importante era que para los nodos del árbol, excepto las hojas, había que procesar a sus hijos menores.Procesar implica checar que colores puede tener un nodo. Por lo que para lograr los puntos en este subcaso era necesario procesar los nodos hijos, luego sus padres y asi sucesivamente. Es decir para procesar, un nodo primero hay que procesar a todos sus hijos.
La forma de procesar a un nodo es la siguiente. Por cada nodo se compara con su padre y al momento de comparar, lo que se busca es que por cada color del nodo, el padre no tenga un color que lo elimine como opción. Es decir tengo el siguiente caso
Nodo -> Rojo, Verde, Azul
Padre -> Rojo, Verde
Por cada color del nodo, el padre puede elegir un color distinto. Por ejemplo, si el Nodo es Rojo, el padre puede ser Verde. Si el nodo es Verde, el padre puede ser Rojo y si el nodo es Azul, puedes elegir el Rojo o el Verde. Sin embargo, para el siguiente caso
Nodo -> Rojo, Verde, Azul
Padre -> Rojo
El padre del nodo solo puede ser Rojo, por lo que para que las condiciones del problema se cumplan, el Nodo no puede ser Rojo. En este caso actualizamos la tabla de valores posibles del Nodo. Y queda como
Nodo -> Verde, Azul
Padre -> Rojo
Lo anterior se hace para cada par de nodos desde los nodos hoja hasta la raíz. Procesandolos de menor a mayor da la mejor solución
Subcaso 3(20 puntos)
Para obtener los puntos del subcaso 3 era posible simplemente ver por cada nodo procesarlo comenzando en la raíz, ya que en este caso el grafo en basicamente una gran línea. Utilizando la técnica descrita en el subcaso 2 por cada nodo se obtenía una solución a este subcaso
Subcaso 4(50 puntos)
Para los puntos del cuarto caso era necesario “linearizar” el grafo, esto simplemente significa que los nodos mas arriba van a tener menor prioridad que los nodos de abajo, es decir el nodo raíz tendría valor 0 mientras que sus hijos tendrían valores más altos. Por ejemplo para un caso asi:
0 -> 1 -> 4
-> 2
-> 3
El nodo 0 es la raíz del árbol, el nodo 1 y 3 son hijos de 0 y los nodos 2 y 4 son hijos de 1, el arbol se linearizaría de la siguiente manera:
0 -> 1, 1 -> 2, 3 -> 3, 4 -> 4, 2 -> 5
Ahora lo que es necesario hacer es por cada nodo de mayor prioridad a los de menor prioridad es necesario hacer la técnica explicada en el subcaso 2.Tomando en cuenta otra observación. Que solo es necesario procesar los nodos que solo tengan un color. Es decir si el nodo 0 tiene posibilidad de ser Rojo, Azul o Verde, no es necesario procesarlo. Sin embargo si un nodo solo puede ser azul, hay que eliminar esa posiblidad tanto de su padre como de sus hijos.
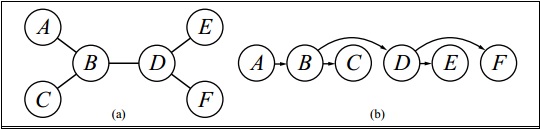
Imagen obtenida de http://aima.cs.berkeley.edu/newchap05.pdf
1 // karbol100.cpp
2 // By Saul de Nova Caballero
3
4 //Librerias de la standard template library de c++(stl)
5 #include <algorithm>
6 #include <cassert>
7 #include <cstdio>
8 #include <cstdlib>
9 #include <cstring>
10 #include <iostream>
11 #include <list>
12 #include <utility>
13
14 using namespace std;
15
16 //Iterador sobre estructuras de datos. En este caso listas de la stl
17 #define TR(container, it) \\
18 for(typeof(container.begin()) it = container.begin() ; it != container.end() ; ++it)
19
20 //Definicion de un par de la stl
21 typedef pair<int, int\> pii;
22
23 //Constantes del programa
24 const int MAXN = 10002;
25 const int MAXM = 502;
26 const int MAXMEM = 2\*MAXN;
27
28 //Clase para definir los hijos del arbol
29 //Es una lista con todos los hijos de cada nodo
30 class Graph {
31 public :
32 void addNode(int node, int value) {
33 nodes\[node\].push\_back(value);
34 }
35 list<int\> nodes\[MAXN\];
36 };
37
38 //Clase para cola de las busquedas en amplitud
39 //Es de tipo generica
40 template<class T>
41 class Queue {
42 public :
43 Queue() { init(); }
44 void init() { p1 = 0; p2 = 1; }
45 void push(T val) { memory\[++p1\] = val; }
46 T front() { return memory\[p2\]; }
47 void pop() { p2++; }
48 bool empty() { return (p1 < p2); }
49
50 private :
51 int p1, p2;
52 T memory\[MAXMEM\];
53 };
54
55 //Definicion de todas las variables del programa
56 int N, M, C, //Variables dadas
57 allowedColorsSize\[MAXN\], //La cantidad de colores posibles por nodo
58 parents\[MAXN\], //El padre de cada nodo
59 colorAssigned\[MAXN\]; //El color que le asigne al final al nodo
60 bool allowedColors\[MAXN\]\[MAXM\]; //Una matriz con todos los colores posibles por cada nodo
61 list<int\> nodesOrder; //Una lista ordenada de mayor a menor por la profundidad de cada nodo
62 Graph tree; //Mi arbol
63 Queue<pii> searchDepth; //Una cola para la busqueda
64
65 //Regresa el color valido por cada nodo permitiendo que un nodo no sea de un color
66 int validColor(int node, int constraint = -1) {
67 for(int i = 0; i < M; ++i) {
68 if(allowedColors\[node\]\[i\] && constraint != i) {
69 return i;
70 }
71 }
72 return -1;
73 }
74
75 //Funcion para la lectura de todas las variables y la inicializacion de las estructuras
76 //Los asserts son para probar que el codigo es correcto
77 /\*Guarda en allowedColors los posibles colores por nodo en una matriz\*/
78 void read() {
79 int node, prohibited;
80 scanf("%d%d", &N, &M);
81 assert(1 <= N && N <= MAXN-2);
82 allowedColorsSize\[0\] = M;
83 memset(allowedColors, true, sizeof(allowedColors));
84 for(int k = 1; k < N; ++k) {
85 scanf("%d", &node);
86 assert(0 <= node && node < N);
87 parents\[k\] = node;
88 tree.addNode(node, k);
89 allowedColorsSize\[k\] = M;
90 }
91 scanf("%d", &C);
92 for(int k = 0; k < C; ++k) {
93 scanf("%d%d", &node, &prohibited);
94 assert(0 <= node && node < N && 0 <= prohibited && prohibited < M);
95 if(allowedColors\[node\]\[prohibited\]) { //Checa que los nodos no se repitan ya que se pueden repetir
96 allowedColors\[node\]\[prohibited\] = false;
97 allowedColorsSize\[node\] --;
98 }
99 }
100 }
101
102 /\*Una busqueda en amplitud para "linearizar el árbol"\*/
103 void orderNodes() {
104 searchDepth.push(make\_pair(0, 0));
105 while(!searchDepth.empty()) {
106 pii value = searchDepth.front(); searchDepth.pop();
107 nodesOrder.push\_front(value.first);
108 TR(tree.nodes\[value.first\], it) {
109 searchDepth.push(make\_pair(\*it, value.second + 1));
110 }
111 }
112 }
113
114 /\*Checa por cada nodo de mayor a menor en la linearizacion, los colores posibles por nodo que solo tiene un color posible\*/
115 void enforceArc() {
116 TR(nodesOrder, it) {
117 int currNode = \*it;
118 int parent = parents\[\*it\];
119 if(currNode != 0) {
120 if(allowedColorsSize\[currNode\] == 1 || allowedColorsSize\[parent\] == 1) {
121 if(allowedColorsSize\[parent\] == 1) {
122 swap(currNode, parent);
123 }
124 int color = validColor(currNode);
125 //printf("%d %d %d\\n", currNode, parent, color);
126 if(allowedColors\[parent\]\[color\]) {
127 allowedColors\[parent\]\[color\] = false;
128 allowedColorsSize\[parent\] --;
129 }
130 }
131 }
132 //Si no hay colores posibles, no se puede resolver el mapa
133 if(allowedColorsSize\[currNode\] <= 0) {
134 printf("-1\\n");
135 exit(0);
136 }
137 }
138 //Checa de nuevo si alguno de los colores no puede ser
139 for(int k = 0; k < N; ++k) {
140 if(allowedColorsSize\[k\] == 0) {
141 printf("-1\\n");
142 exit(0);
143 }
144 }
145 }
146
147 //Hace un ciclo checando el menor color posible por nodo e imprime los colores menores
148 void findSolution() {
149 colorAssigned\[0\] = -1;
150 list<int\>::iterator it = nodesOrder.end();
151 do {
152 it --;
153 assert(0 <= \*it && \*it < N);
154 int color = validColor(\*it);
155 if(colorAssigned\[parents\[\*it\]\] == color) {
156 color = validColor(\*it, color);
157 }
158 assert(0 <= color && color < M);
159 colorAssigned\[\*it\] = color;
160 } while(it != nodesOrder.begin()) ;
161
162 for(int k = 0; k < N; ++k) {
163 printf("%d\\n", colorAssigned\[k\]);
164 }
165 }
166
167 int main() {
168 read();
169 orderNodes();
170 enforceArc();
171 findSolution();
172 return 0;
173 }