Solución a "Contraseña Binaria"

Concurso: Preselectivo para la IOI 2015, Etapa 1, Problemset 7 Autor: Orlando Isay Mendoza Garcia Fuente: Christian Adan Hernández Sánchez

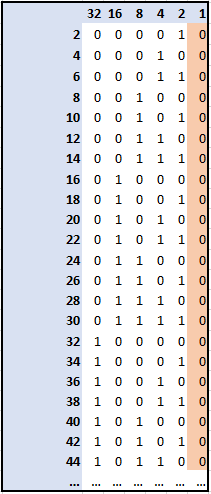
Podemos ayudarnos de la imagen para comprender mejor esta explicación:

En ella aparecen de forma descendente a la izquierda los números pares comenzando desde el dos, y su representación binaria a la derecha. En la parte superior aparece el valor de cada cifra en decimal.

Tomando en cuenta el límite del problema, sabemos que si sumamos $latex B(i)$ para cada par menor o igual a $latex N$, en el peor de los casos tendríamos que realizar 500,000,000,000,000 veces la función. Aún si lograramos calcularla en una operación nuestro programa excedería el tiempo límite.

En cambio, haciendo cálculos notamos que: $latex 2^{50} \approx 1,000,000,000,000,000$. Lo cual significa que a lo más habrán 50 columnas en la tabla (ya que en la forma binaria cada cifra representa una potencia de 2).

Dado que sabemos que en una suma el orden de las cantidades a sumar no importa, podemos determinar que es lo mismo sumar los valores de forma horizontal, tanto como de forma vertical. Sumando los valores de las columnas solo tomaría 50 operaciones. La columna 1 podemos ignorarla ya que al ser pares los números de la lista ninguno contendrá un 1 en la última cifra.

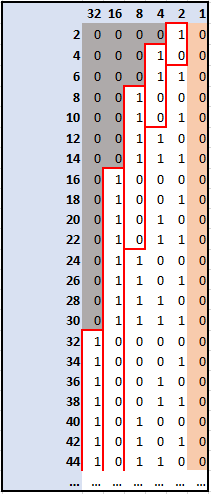
Observando la siguiente imagen, vemos que la columna $latex C$ se forman grupos de tamaño $latex C$ (por ejemplo, en la columna 4 se forman grupos de cuatro elementos),que contienen una la mitad de $latex 1$s y la otra de $latex 0$s. También podemos ver que en la columna 2 no hay $latex 0$s antes del primer grupo, en columna 4 hay un 0, en la que sigue hay 2, luego 4,etc (área en color gris). Podemos notar que ese espacio aumenta en base a potencias del dos.

Teniendo el número $latex N$ habrán $latex N / 2$ números en la lista. Para calcular la cantidad de grupos completos que se forman en cada columna dividimos $latex N$ menos el espacio lleno de ceros en esa columna, entre el número de la columna en el que estemos; a su vez, esta cantidad la multiplicamos por, el número de la columna entre dos. Sin embargo, puede que nos falten de contabilizar los $latex 1$s que pudieran estar en un grupo que no se completo. Esto se arregla sumando a lo anterior, el mínimo entre el resto de la división anterior y, el número de la columna entre dos.

Código: