Solución a "Alfiles"
Concurso: Preselectivo para la IOI 2013, Etapa 1, Examen 7 **Autor: **Hugo Dueñas
Lo primero que se debe de notar es que en cada una de las $latex 2n-1$ diagonales principales, las cuales mostradas en la imagen de abajo, habrá máximo 1 alfil. Lo mismo se cumple para las diagonales invertidas, mostradas también en una imagen abajo.
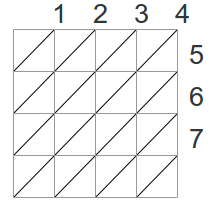
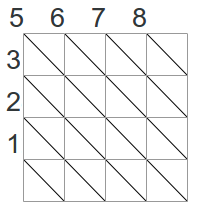
Ahora, cada diagonal principal se cruza con ciertas diagonales invertidas. Entonces se plantea una solución de tipo Backtracking que corre sobre las diagonales principales marcando diagonales invertidas a cada paso (representando que se ha colocado un alfil en el cruce de esas dos diagonales).
Una implementación directa y sin optimizaciones ni podas para los casas donde $latex n = 8$ hará uso de $latex 1\times2\times3\times4\times5\times6\times7\times8\times7\times6\times5\times4\times3\times2\times1=203212800$ operaciones, lo cual no está muy lejos de ser una solución eficiente. Entonces bastan algunas podas para obtener una solución al 100%, podemos por ejemplo podar las ramas de la recursión que consideran combinaciones con una diagonal invertida repetida.
A continación se lista una implementación en C++ de la solución: