Invasion Zombie

Hola!, este es mi primer post en Omegaup y voy a describir mi solución para el problema Invasion zombie. Hace un año encontré este problema, me pareció interesante y logre resolverlo, aunque algo tricky. Hace unos días me tope con este problema nuevamente y lo resolví por segunda ocasión, pero con una solución más simple, al menos eso creo.

Primer solución

La idea principal tanto en la primera como en la segunda solución es diseñar una función $latex f(d)$ que nos retorne el número de colonias infectadas después de $latex d$ días, nos interesa el mínimo valor de $latex d$ tal que el número de colonias infectadas sea mayor o igual a $latex C$. Una propiedad importante es la siguiente, $latex f(d)$ nunca decrece, es decir $latex f(d) <= f(d+1)$. Esta propiedad nos permite utilizar búsqueda binaria para encontrar las respuesta en $latex O(\lg_{2}(n))$. Diseñar una función que determine el número de colonias infectadas, dependiendo del background de cada uno, es la parte interesante, y es donde difieren las dos versiones, bueno, un poco. Este es el código de la primer versión, no voy a entrar en detalles porque ni yo me acuerdo bien que trucos aplique, pero la idea es parecida a la de la de la segunda versión, lo que cambia es la estrategia.

Segunda versión

Bueno, empecemos, trascurridos $latex d$ días, ¿cuántas colonias han sido infectadas? Simulemos la invasión y veamos si podemos encontrar un patrón. 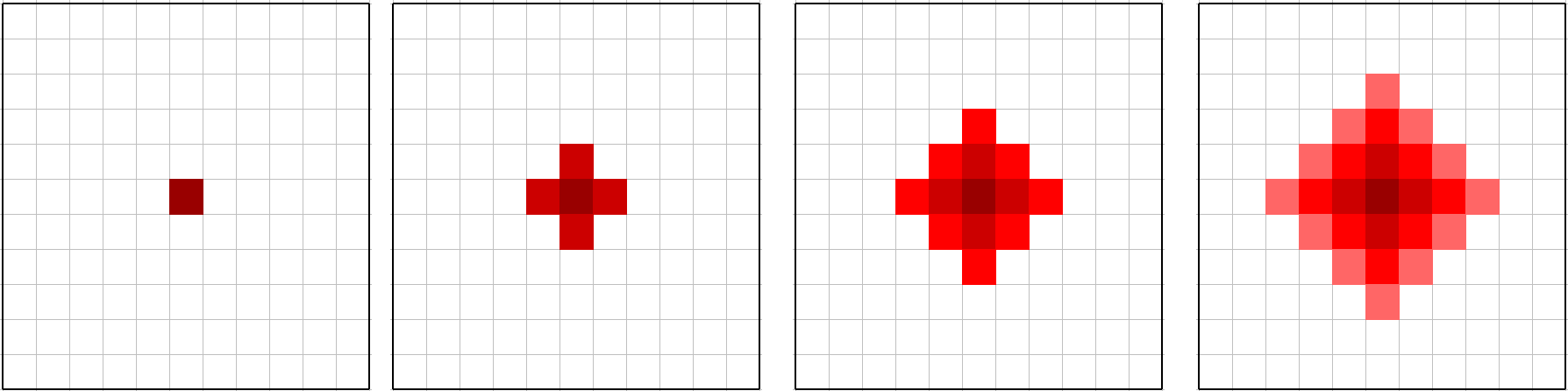No es complicado llegar a la siguiente fórmula: $latex f(d) = d^{2} + (d+1)^{2}$ Si el espacio de la ciudad fuese ilimitado nuestra función de verificación sería algo parecido a:

Sin embargo, el espacio de la ciudad es limitado y habrá casos como los siguient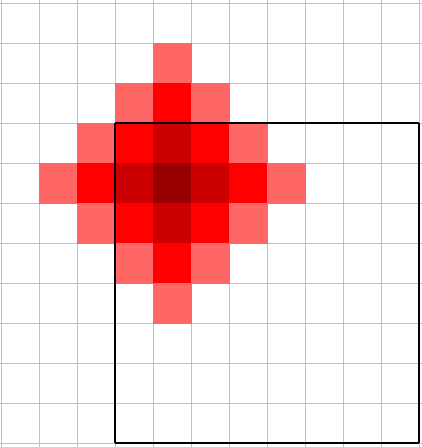es: Entonces nuestro objetivo es encontrar el área delimitada por la ciudad (un cuadrado de N * N unidades), lo cual se pone un poco tricky. La siguiente imagen nos ayudará a entender el código de la solución sin entrar en tantas explicaciones. 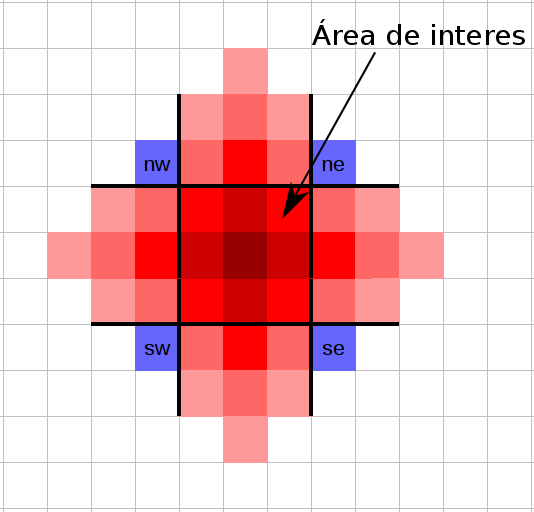Es decir, el área total menos el área de los triángulos superior, inferior, izquierdo y derecho. Obsérvese que los triángulos pueden traslaparse y por lo tango estaríamos restando esas áreas 2 veces, por ello tenemos que calcular las áreas de traslape (nw, ne, se y sw en la imagen) y regresar lo a la suma total. Lo que sigue es la implementación:

Espero que les sea útil, dudas, comentarios o correcciones son bienvenidas.